Fast Approximation to Spherical Harmonic Rotation
Proceedings of
Spring Conference on Computer Graphics, pp. 51-58, 2006
Rotation of functions represented by spherical harmonics is an
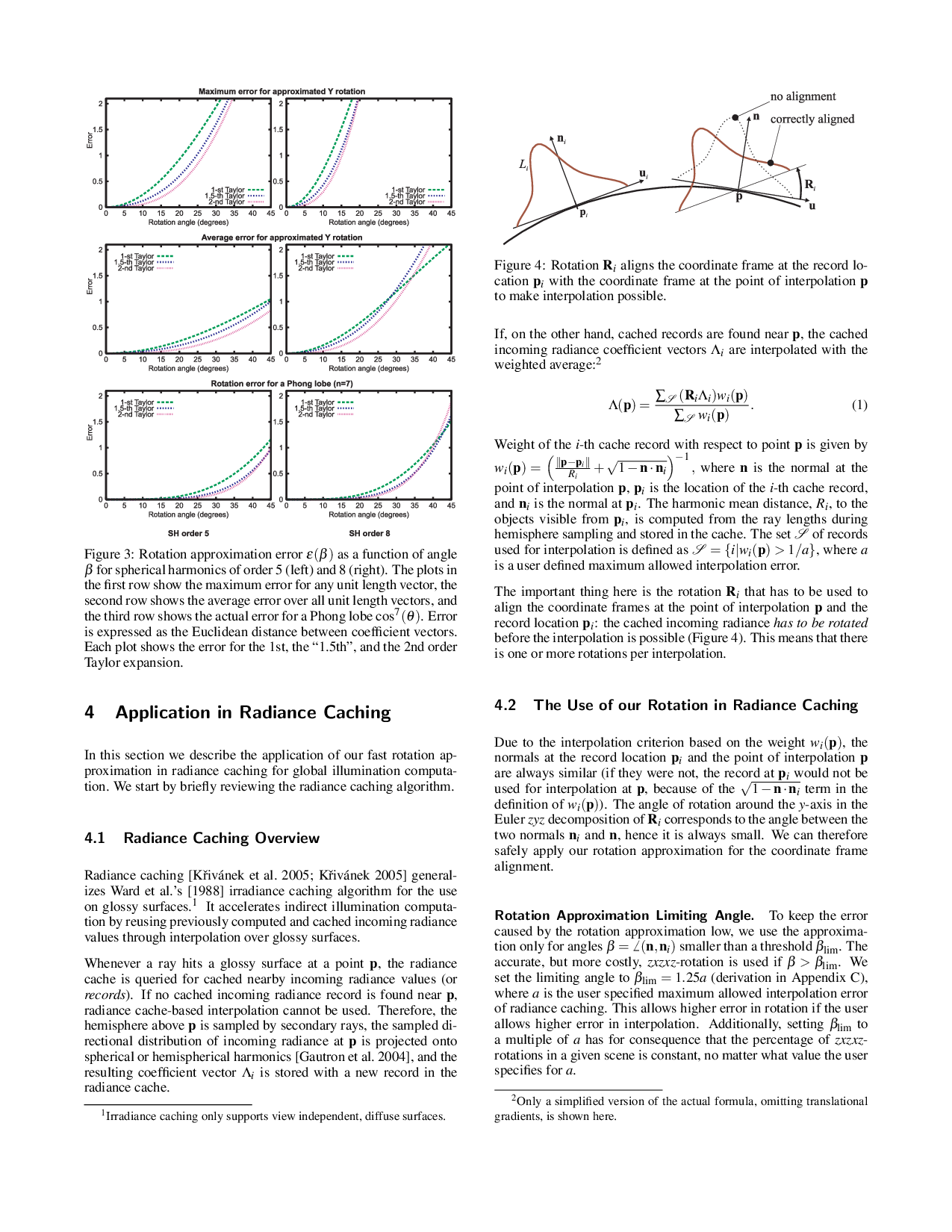
important part of many real-time lighting and global illumination algorithms.
For some of them a per-vertex or even per-pixel rotation is required, which
implies the necessity of an efficient rotation procedure. The speed of any of
the existing rotation procedures is, however, not able to meet the requirements
of real-time lighting or fast global illumination. We present an efficient
approximation of the spherical harmonic rotation applicable for small rotation
angles. We replace the general spherical harmonic rotation matrix by its
truncated Taylor expansion, which significantly decreases the computation
involved in the rotation. Our approximation decreases the asymptotic complexity
of the rotation---the higher the order of spherical harmonics, the higher the
speed-up. We show applications of the proposed rotation approximation in global
illumination and real-time shading. Although the rotation approximation is
accurate only for small rotation angles, we show this is not a serious
limitation in our applications.